Dringende Frage (vollständige Induktion)

Zuckerschnute

Zuckerschnute

Member
Registriert
Dezember 2001
Alter
39
Ort
Mülheim an der Ruhr
Geschlecht
w

Hallo zusammen!

Es mag ungewöhnlich klingen, aber in der letzten Deutschstunde haben wir zu Beginn ein wenig Mathe gemacht. :)
Ihr kennt sicher alle die Geschichte mit dem Philosophen und dem Bauern, die Schach spielen?
Der Bauer verliert ständig und der Philosoph schlägt ihm dann vor, auf jedes Schachfeld immer doppelt so viel Reis zu tun. Also auf das erste 1 Korn, auf das zweite 2, dann 4, dann 8 etc.
Dann darf der Bauer sich aussuchen, ob er die ersten 63 Felder will oder nur das 64te. Der Bauer entscheidet sich für die ersten 63, da er denkt, dass diese mehr seien als nur das 64te.

So, jetzt sollen wir als Hausaufgabe mit vollständiger Induktion zeigen, dass eben auf dem 64ten Feld mehr Reiskörner sind als auf den ersten 63 Feldern zusammen.

Er hat uns den Ansatz:

a^n>a^n-1+a^n-2+a^n-3

genannt, der aber irgendwie nicht stimmen kann...

Habt ihr vielleicht eine Idee, ich habe nämlich nicht die geringste Ahnung, da wir das Thema in Mathe auch nur kurz angeschnitten hatten...

Danke im Voraus! :ciao:
 
Da n ist in dem Fall 64, weil es 64 Felder auf dem Schachbrett sind und es eben nicht mehr gibt. n-1 wär dann also 63. Man rechnet jetzt 2^64 und dann hat man die höchste Zahl. Diese ist höher als alle anderen zusammen. Ich hoffe ich konnte die weiter helfen!
;)
 
64, weil es 64 Felder auf dem Schachbrett gibt. und 2 weil es immer verdoppelt wird. Also 2 hoch 64! Ich habs auch grad nach gerechnet. Da kommt dann so eine bombastische Zahl von

18446744073709551616

raus!
 
Vollstängige Induktion ist zwar schon länger her, aber ich wills mal versuchen:

Schachbrett
1. Feld a^0=1
2. Feld a^1=a
...
64. Feld a^63

Vorausetzung : a >1, n >= 0

Ansatz a^n > a^n-1+a^n-2+ ...+ a^0

erster Schritt:

n=0

a^0 > a^-1 = 1/a richtig. für a>1

n=1
a^1 > a^0 = 1 richtig

zu beweisen a^n > a^n-1+a^n-2+ ...+ a^0
Induktionsannahme: was für n gilt, gilt auch für n+1.

a^n+1 > a^n+a^n-1+a^n-2+ ...+ a^0
Die rechte Seite kann man umschreiben zu
a^n+1> a (a^n-1+a^n-2+ ...+ a^0) + a^0
Kürzen mit a***
a^n > (a^n-1+a^n-2+ ...+ a^0) + a^-1
oder
a^n -a^-1 >= (a^n-1+a^n-2+ ...+ a^0)
daraus folgt

a^n > (a^n-1+a^n-2+ ...+ a^0) da a^n > a^n- a^-1
qed

Vielleicht wird es damit etwas verständlich. Auch wenn der Bauer nur ein Reiskorn mehr bekommen hätte.

PoohBear

Edit: ***Merke gerade da ist noch ein kleiner Denk- bzw. Rechenfehler drin.

Edit2: Der Rechenfehler ist jetzt draussen.
Die exakte Lösung ist a^n -1 = a^n-1+a^n-2+ ...+ a^0, lässt sich im binären Zahlensystem leicht zeigen.
 
Zuletzt bearbeitet:
Damit wär deine Frage wohl beantwortet. :)
 
Original geschrieben von PoohBear
Die rechte Seite kann man umschreiben zu
a^n+1> a (a^n-1+a^n-2+ ...+ a^0) + a^0
Kürzen mit a***
a^n > (a^n-1+a^n-2+ ...+ a^0) + a^-1
oder
a^n -a^-1 >= (a^n-1+a^n-2+ ...+ a^0)
daraus folgt

a^n > (a^n-1+a^n-2+ ...+ a^0) da a^n > a^n- a^-1
qed
Zum Vergrößern anklicken....

Doch noch ne Frage. :rolleyes: Wieso kann man die rechte Seite so umschreiben? Wenn man die Klammer an der Stelle zusammen fassen würde, hätte man doch a² ... ?

:confused:
 
@Zuckerschnute

Machen wir mal ein Beispiel, ist vielleicht etwas anschaulicher
n=3, n+1 = 4:

I: a^4 > a^3 + a^2+a^1+a^0

Aus den ersten drei Termen auf der rechten Seite kann man a ausklammern

II: a^3 + a^2+a^1 = a*(a^2+a^1+a^0)

ergibt also

a^4 > a*(a^2 + a^1 + a^0) + a^0

Man muß also in der Klammer vom Exponenten immer 1 abziehen n-->n-1, n-1 -->n-2 bis man bei 0 angekommen ist. (daher bleibt der a^0 Term der Gleichung I übrig). Der Vergleich mit dem Ansatz (a^n-1 + a^n-2 +... + a^0) zeigt dann genau dieselbe Form, erweitert um a* bzw. die konstante a^0. Kürzen mit a und Umstellen liefert dann die Lösung

III: a^3 - 1/a > a^2 + a^1+ a^0 oder eben
IV: a^3 > a^2 + a^1+ a^0 weil a^3 > a^3 - 1/a

Ich hoffe ich hab's einigermaßen verständlich erklärt.

PoohBear
 
Also sind die ersten 63 Felder doch mehr als nur das 64te? Weil du meintest, der Bauer hätte nur ein Reiskorn mehr bekommen... Unser Lehrer meinte aber, das 64te Feld wäre mehr als die ersten 63...
 
@Zuckerschnute

Auf dem Schachbrett liegen genau (2^64) - 1 Reiskörner, hätte der bauer 2^64 haben wollen, hätte er genau eines mehr bekommen.
Läßt sich leicht im binären Zahlensytem zeigen:

7 = 2^2 + 2^1 + 2^0 = 111
1 = 2^0 = 001

Beide addieren ergibt:
111
+ 001
---------
1000

Ergibt also 2^3 = 8 oder anders herum 2^3 -1 = 2^2+2^1+^2^0

Und 2^64-1 ist eine ziemlich große Zahl.

Zum Beispiel hier (in den Randspalten)
http://www.fonline.de/rs-ebs/algebra/alg18.htm
Mit ein paar Überlegungen, wieviel Tonnen Reis das ergibt.

PoohBear
 
Ach so, ja dann ist alles klar... glaub ich. :p
Muss das mal in Ruhe nachvollziehen. Den letzten Schritt hab ich noch nicht ganz verinnerlicht. ;)

EDIT: Warum ist die Voraussetzung a>1 und n>=0 ??? Also warum weiß ich schon, aber wie kann ich das erklären? Denn dann ist das Verfahren ja nicht allgemein gültig?!
 
Zuletzt bearbeitet:
@Zuckerschnute

Hab mir nochmal die Aufgabenstellung von Deinem Lehrer angeschaut. Die Aufgabe ist Standard in der Algebra und man kann noch ein paar spielchen damit machen.

Wenn man sich natürchlich zwischen dem 63. und 64. Feld entscheiden soll, dann gilt natürlich

Feld 1 bis 63 zusammen ergibt (2^63) -1 = 9223372036854775807 Reiskörner
Feld 64 hat 2^63 = 9223372036854775808 Reiskörner

ändert aber nichts an der tasache, dass er nur ein reiskorn mehr bekommt.

PoohBear
 
Original geschrieben von Zuckerschnute
EDIT: Warum ist die Voraussetzung a>1 und n>=0 ??? Also warum weiß ich schon, aber wie kann ich das erklären? Denn dann ist das Verfahren ja nicht allgemein gültig?!
Zum Vergrößern anklicken....

Warum sollte das Verfahren nicht mehr gültig sein.

a = 1 ist nicht besonders sinnvoll, weil 1^n ergibt immer 1, und man hätte genau 64 Reiskörner auf dem Schachbrett. Außerdem trifft die Bedingung a^0 > a^-1 im Falle von a=1 nicht mehr zu!

n kleiner Null zuzulassen, führt dazu das man auf jedem Feld das Reiskorn teilen muß, erst 1, 1/2, 1/4, .... Spätestens am 64. Feld hat man ein Problem. Aber Konvergenzprobleme endlicher Reihen geht - glaube ich - etwas über den Schulstoff hinaus.;)

PoohBear
 
Original geschrieben von Zuckerschnute
Wie kommst du auf diesen Schritt? Wenn ich n=1 setze, hätte ich:
a^1 > a^0 + a^-1 + ... + a^0

Würde ich dann beispielsweise für a 2 einsetzen, würde die Aussage nicht mehr stimmen...

:confused:
Zum Vergrößern anklicken....

Da machst du jetzt ein kleinen Denkfehler, man fängt bei n an und hört bei 0 auf

n=1; n-1 = 0.

a^1 > a^0 : Probe 2^1 > 2^0 = 2 > 1

n=3; n-1 = 2, n-2 = 1, n-3 = 0.
a^3 > a^2 + a^1 + a^0 : Probe 2^3 > 2^2 + 2^1 +2^0 = 8 > 7

Der Term a^-1 ergibt sich nur im Beweis.

PoohBear
 
Verstehe ich nicht. :confused:

Wir hatten ja

a^n > a^n-1 + a^n-2 + a^n-3 ... a^0

Und wenn ich da dann n=1 einsetze habe ich doch:

a^1 > a^1-1 + a^1-2 + a^1-3 ... a^0

oder nicht? Und warum bleibt dann nachher nur noch

a^1 > a^0 ?
 
Original geschrieben von Zuckerschnute
Verstehe ich nicht. :confused:

Wir hatten ja

a^n > a^n-1 + a^n-2 + a^n-3 ... a^0

Und wenn ich da dann n=1 einsetze habe ich doch:

a^1 > a^1-1 + a^1-2 + a^1-3 ... a^0

oder nicht? Und warum bleibt dann nachher nur noch

a^1 > a^0 ?
Zum Vergrößern anklicken....

a^n > a^n-1 + a^n-2 + a^n-3 ... + a^0 ist die allgemeine Formel für beliebiges n.

Man bricht aber solche Reihen ab, wenn der Exponent Null ist. Und damit ist bei n=1, gleich nach dem ersten Summanden Schluß, weil mit negativen Exponenten gibt es das absolute Chaos.

a^1 > a^1-1 = a^0 = 1

Deine Lösung würde ja heißen z.B a = 2

2^1 > 2^0 + 2^-1+ 2^-2+ ... + 2^0= 1 + 1/2 + 1/4 + ... + 1 = 2, 9...

Auf dem 1. Feld liegt aber nur ein ganzes Reiskorn.;)

PoohBear

Edit: Man muss unterscheiden zwischen unseren normalen Nummerierungsmethoden. Im täglichen Leben fängt man bei 1 an und hört bei 64 auf. Mathematisch muß man mit 0 (Null) anfangen und hört bei 63 auf.
 
Zuletzt bearbeitet:
@Zuckerschnute

Gern geschehen, war mal auch eine Abwechslung zum langweiligen Büroalltag.:)

PoohBear
 
So, hab meinem Lehrer die Aufgabe gezeigt. Ich glaub da hab ich mit gepunktet. ;) Er hat mir dann seine Lösung gegeben, ich soll die mal durchschauen. :)

Und jetzt ratet mal.... Er hat einfach von Anfang an für a = 2 eingesetzt...

Aber dann ist es ja eigentlich nicht allgemein bewiesen oder? Toll, so leicht hätte ich es mir auch machen können.

Egal, ich habe jetzt gleichzeitig noch was für Mathe getan, dank vor allem dir, PoohBear!

Nochmal danke für alles! :hallo:
 
@Zuckerschnute

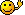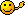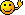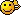
:lol: Das zeigt doch wiedermal, wie einfach man/frau einen Lehrer austricksen kann.:lol:

Gemeinsam haben wir den allgemeinen Beweis geliefert. Damit hat dein Lehrer sicher nicht gerechnet und er hat hoffentlich auch noch etwas dazu gelernt.;)

PoohBear
 
Du musst dich einloggen oder registrieren, um hier zu antworten.

Zur Zeit aktive Besucher

Gesamt: 1 (Mitglieder: 0, Gäste: 1)
Zurück
Oben Unten