Ich kann leider nicht helfen, habe aber auch eine dringende Bitte!
Könnte mir jemand erklären, was die zentrische Streckung ist oder mir einen Link zu 'ner guten Seite schicken?
Danke schonmal
LG
S.I.M.S.
Dieses
Bild zeigt's sehr schön. Letztlich ist es nicht mehr als ne Vergrößerung. Die Strecken verhalten sich immer gleich zueinander, also
[Strecke(ZA) / Strecke (ZA')] = [Strecke(ZB) / Strecke (ZB')] = [Strecke(ZC) / Strecke (ZC')]
Hier gibt's ne kleine Erklärung.
____________
Ich hab auch mal ne Frage, evlt. sind ja einige Mathematiker hier. Ich hab ein Problem mit Analysis IV / Integrationstheorie. Übungsaufgabe stammt von diesem
Blatt / Aufgabe 1.
Aufgabe 1. (5 Punkte)
Sei f : R² → R³ eine lineare Abbildung gegeben durch die Darstellungsmatrix a(ij) bezüglich der Standardbasen. Seien α(1), α(2) und β(1), β(2), β(3) die dualen Basen. Berechne:
f*ω für ω = β(i) und ω = β(i)∧ β(j)und ω = β(1)∧β(2)∧β(3).
bisher hab ich, dass f ja ne 2x3 Matrix ist, da linear wie genannt. Als natürliche Basis hab ich in R² {[1,0], [0,1]}. Damit krieg ich dann
f([1,0]) = (a12, a12, a13)
damit dachte ich dann, dass
f*ω([1,0], [0,1]) = ω([a11, a21, a31], [a21, a22, a32]
ist. Damit sollte dann f*β(i) doch so aussehen:
f*β(i) = (ai1, ai2)
Oder? Und wie sehen die anderen aus? Ich kapier die Notaton mit "∧" nicht...

/edit: ich glaube ich hab's gelöst:







 oder so etwas
oder so etwas 

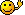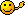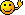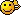

 Wär sonst peinlich für einen von uns geworden.
Wär sonst peinlich für einen von uns geworden.  Hast du ne Idee ?
Hast du ne Idee ?